質譜專文 Technical Articles:淺談離子阱解析度
3224
次閱讀
次閱讀
淺談離子阱解析度
林俊利 中央研究院 基因體研究中心 研究助技師
撰於 2012.10.31
林俊利 中央研究院 基因體研究中心 研究助技師
撰於 2012.10.31
質譜儀已被廣泛應用於各個領域,尤其以液相層析串接離子阱質譜儀(LCMS)最為分析人所使用,因具有MSn多次氣體碰撞裂解(collision induced dissociation)的功能,根據碎片質量推測出原始分子離子的結構。離子阱質譜的分析原理是依據Mathieu equation所導出的穩定區圖(stable diagram),由於離子於z軸方向在不穩定區具有質量選擇性拋出的特性,離子阱質譜根據此特性被廣泛使用於分子的質量的量測與結構的鑑定。利用改變固定頻率的振幅,使的z軸方向產生不穩定,而在穩定區的邊界不同荷質比的離子被依序拋出。因為是量測質量因此量測的解析度就被受重視,今日的離子阱質譜都已經採用共振拋出(resonance ejection)的方法來提高解析度,所謂共振拋出是在離子進入離子阱是以環電極(ring electron)上的正弦波電壓與頻率來限制住特定荷質比範圍的離子,此時離子軌跡符合Mathieu equation的參數規範qz小於0.908,若是此時在端蓋板(end cap)加上小電壓的AC,此時離子在離子阱內迴旋頻率與加在end cap上的頻率相同,qz值相同,離子吸收額外的能量增加在z軸方向的振幅,最終振幅大於環電極中心至端蓋板距離Z0,離子被拋出離子阱之外,由於離子阱之有有與離子電性相反的conversion dynode與電子倍增器,離子被具高壓電的金屬板 (conversion dynode)吸引最終撞擊其表面,產生二次電子與二次離子,推向電子倍增器,二次電子與離子撞擊電子倍增器(Electron Multiplier)表面放大訊號,由類比轉數位器(ADC)記錄訊號強度。共振拋出是讓相同荷質比的離子在相同的qz值同時被拋出沒有延遲的問題,造成解析度下降。
今天所要探討的是造成離子阱質譜儀解析度下降的原因,影響解析度的因素有許多,如氣體壓力,氣體分子種類,掃瞄速度,共振拋出,離子阱幾何結構,正弦波頻率及電壓,位能阱深度,表面精度等會影響離子阱的解析度,目前所要討論的是在不穩定拋出(mass-selective instability)的條件下,離子阱幾何結構所產生的高次項電場對非線性離子阱所造成的影響,經由數學運算找出提高解析度的方法。
電場在離子阱內以球型座標表: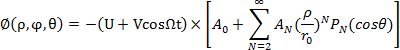 V與W是分別是正弦波的電壓(0-peak)與頻率,U是加在環電極上的直流電壓(DC),是Legendre多項式,r0是環電極的半徑,AN是無因次單位是由場造成。
V與W是分別是正弦波的電壓(0-peak)與頻率,U是加在環電極上的直流電壓(DC),是Legendre多項式,r0是環電極的半徑,AN是無因次單位是由場造成。
An的表示式以球型座標表示,這裏只表示到八極場: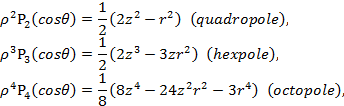 在純四極場(quadropole)中,A0=-0.5,A1=0因是隅極,A2是四極,其他A3=A4=…=0。高次項的不均勻電場來自於離子阱幾何結構與環電極挖洞及端蓋板挖洞所產生,離子阱幾何結構如圖所示,不同漸近線截斷距離就會產生不同大小的高次項。
在純四極場(quadropole)中,A0=-0.5,A1=0因是隅極,A2是四極,其他A3=A4=…=0。高次項的不均勻電場來自於離子阱幾何結構與環電極挖洞及端蓋板挖洞所產生,離子阱幾何結構如圖所示,不同漸近線截斷距離就會產生不同大小的高次項。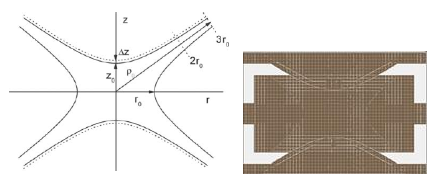
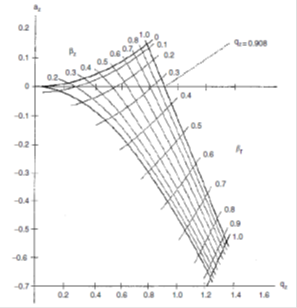 因為離子阱只有RF正弦波電壓,沒有DC直流電壓,如上圖az=0,荷質比只與qz有關,線性的Mathieu equation與正弦波表示如下,
因為離子阱只有RF正弦波電壓,沒有DC直流電壓,如上圖az=0,荷質比只與qz有關,線性的Mathieu equation與正弦波表示如下,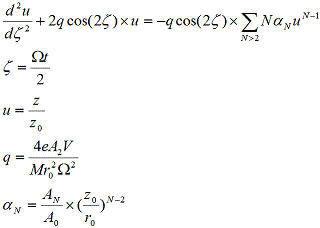 由於Mathieu equation只有數值解,沒有解析解,因此利用數值分析軟體幫助我們計算二階微分方程,目前較多人利用的軟體為Matlab,使用軟體內四階Runge-kutta方法做數值解。
由於Mathieu equation只有數值解,沒有解析解,因此利用數值分析軟體幫助我們計算二階微分方程,目前較多人利用的軟體為Matlab,使用軟體內四階Runge-kutta方法做數值解。
舉例說明,離子阱的正弦波頻率為,在掃瞄時,正弦波的電壓的隨著時間變化,時間就是掃瞄的速度,如掃瞄速度為5555Da/s,而荷質比由180變化到190 ,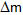 為10,則掃瞄10Dalton的變化所需電壓變化時間為,10*(1/5555)=0.018秒,而變化10Da所需改變的電壓由
為10,則掃瞄10Dalton的變化所需電壓變化時間為,10*(1/5555)=0.018秒,而變化10Da所需改變的電壓由
m/z 180; (0.908*0.18*0.0001*(2*3.1415*1000000)^2)/(4*1.602E-19*6E+23)=1678.1V
m/z 190; (0.908*0.19*0.0001*(2*3.1415*1000000)^2)/(4*1.602E-19*6E+23)=1771.3V
電壓由1678.1變化到1771.3伏特。
對於特定離子185m/z,當正弦波電壓由1678.1變化到1771.3V,其qz值的變化由電壓
1678.1V;
(4*1.602E-19*6E+23*1678.1)/(0.185*0.0001*(2*3.1415*1000000)^2)=0.8834
1771.3V;
(4*1.602E-19*6E+23*1771.3)/(0.185*0.0001*(2*3.1415*1000000)^2)=0.9325
只有純四極場的在Matlab表示如下 function dy=func13_4(t,y)
function dy=func13_4(t,y)
q=0.88+((0.923-0.88)/0.0018)*t
dy=[y(2);-((2*pi*1e6)^2/2)*q*cos(2*pi*1e6*t)*y(1)];
在Matlab內執行
>> ode45('func13_4',[0,0.001215],[0.01,0])
>> [t,y]=ode45('func13_4',[0,0.001215],[0.01,0]);
>> whos y
>> plot(t,y(:,1));legend('y1(t)')
初始條件為
Z(t)=0.01, t=0; 離子在t=0,z軸上啟始位置
Z(t)’=0, t=0; 離子速度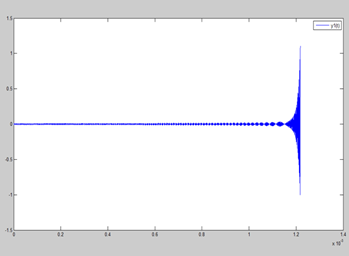 上圖縱軸是Z(t)/Z0,橫軸是時間對應是qz的變化
上圖縱軸是Z(t)/Z0,橫軸是時間對應是qz的變化
qz=0.88+((0.923-0.88)/0.0018)*t;
qz , 185m/z
=0.8834+((0.9325-0.8834)/0.0018)*0.001218
=0.91667
當octopole值為 +1%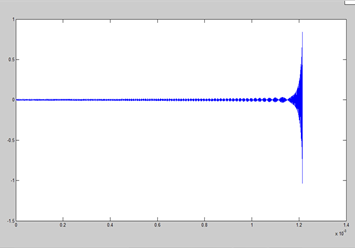 qz , 185m/z
qz , 185m/z
=0.8834+((0.9325-0.8834)/0.0018)*0.001215
=0.91658
當octopole值為 -1%
function dy=func13_6(t,y)
q=0.88+((0.93-0.88)/0.0018)*t
dy=[y(2);-((((2*pi*1e6)^2)/2)*q*cos(2*pi*1e6*t)*y(1))+((((2*pi*1e6)^2)/4)*q*cos(2*pi*1e6*t)*4*0.01*y(1)^3)];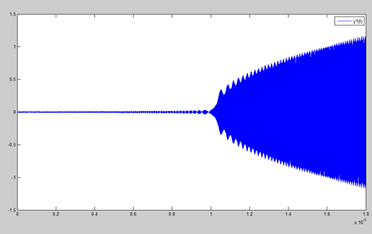 qz , 185m/z
qz , 185m/z
=0.8834+((0.9325-0.8834)/0.0018)*0.001215
=0.91658
當加入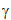 項時且octopole值為 -1%,Mathieu equation的表示如下;
項時且octopole值為 -1%,Mathieu equation的表示如下;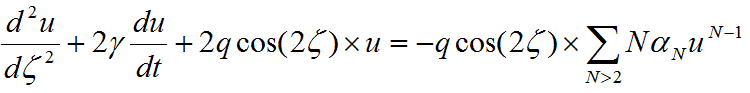
 是氣體阻尼系數(damping)的表示值,大約0.005,不同壓力與氣體分子會有所不同。
是氣體阻尼系數(damping)的表示值,大約0.005,不同壓力與氣體分子會有所不同。
function dy=func13_7(t,y)
q=0.88+((0.932-0.88)/0.0018)*t
dy=[y(2);-((((2*pi*1e6)^2)/2)*q*cos(2*pi*1e6*t)*y(1))-0.005*y(2)+((((2*pi*1e6)^2)/4)*q*cos(2*pi*1e6*t)*4*0.01*y(1)^3)];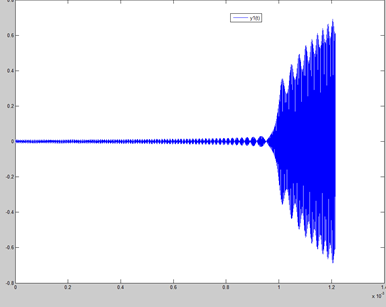
當octopole項為+1%時沒有出現延遲拋出(delay ejection)的問題,這也是為何將end cap的拋物面改成拉伸,z0=0.70711*110.6%=0.78206,如此可以低消end cap挖洞所造成的-1% octopole項。
[2] Z. Nie et al. International Journal of Mass Spectrometry 270 (2008) 8.
[3] Alexander A. Makarov, Anal. Chem., 68, (1996), 4257.
今天所要探討的是造成離子阱質譜儀解析度下降的原因,影響解析度的因素有許多,如氣體壓力,氣體分子種類,掃瞄速度,共振拋出,離子阱幾何結構,正弦波頻率及電壓,位能阱深度,表面精度等會影響離子阱的解析度,目前所要討論的是在不穩定拋出(mass-selective instability)的條件下,離子阱幾何結構所產生的高次項電場對非線性離子阱所造成的影響,經由數學運算找出提高解析度的方法。
電場在離子阱內以球型座標表:
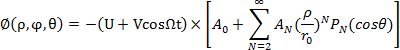
An的表示式以球型座標表示,這裏只表示到八極場:
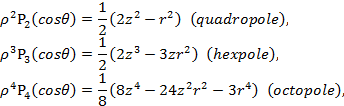


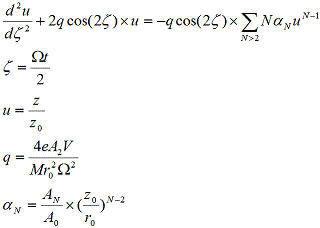
舉例說明,離子阱的正弦波頻率為,在掃瞄時,正弦波的電壓的隨著時間變化,時間就是掃瞄的速度,如掃瞄速度為5555Da/s,而荷質比由180變化到190 ,
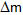 為10,則掃瞄10Dalton的變化所需電壓變化時間為,10*(1/5555)=0.018秒,而變化10Da所需改變的電壓由
為10,則掃瞄10Dalton的變化所需電壓變化時間為,10*(1/5555)=0.018秒,而變化10Da所需改變的電壓由 m/z 180; (0.908*0.18*0.0001*(2*3.1415*1000000)^2)/(4*1.602E-19*6E+23)=1678.1V
m/z 190; (0.908*0.19*0.0001*(2*3.1415*1000000)^2)/(4*1.602E-19*6E+23)=1771.3V
電壓由1678.1變化到1771.3伏特。
對於特定離子185m/z,當正弦波電壓由1678.1變化到1771.3V,其qz值的變化由電壓
1678.1V;
(4*1.602E-19*6E+23*1678.1)/(0.185*0.0001*(2*3.1415*1000000)^2)=0.8834
1771.3V;
(4*1.602E-19*6E+23*1771.3)/(0.185*0.0001*(2*3.1415*1000000)^2)=0.9325
只有純四極場的在Matlab表示如下

q=0.88+((0.923-0.88)/0.0018)*t
dy=[y(2);-((2*pi*1e6)^2/2)*q*cos(2*pi*1e6*t)*y(1)];
在Matlab內執行
>> ode45('func13_4',[0,0.001215],[0.01,0])
>> [t,y]=ode45('func13_4',[0,0.001215],[0.01,0]);
>> whos y
>> plot(t,y(:,1));legend('y1(t)')
初始條件為
Z(t)=0.01, t=0; 離子在t=0,z軸上啟始位置
Z(t)’=0, t=0; 離子速度

qz=0.88+((0.923-0.88)/0.0018)*t;
qz , 185m/z
=0.8834+((0.9325-0.8834)/0.0018)*0.001218
=0.91667
當octopole值為 +1%

=0.8834+((0.9325-0.8834)/0.0018)*0.001215
=0.91658
當octopole值為 -1%
function dy=func13_6(t,y)
q=0.88+((0.93-0.88)/0.0018)*t
dy=[y(2);-((((2*pi*1e6)^2)/2)*q*cos(2*pi*1e6*t)*y(1))+((((2*pi*1e6)^2)/4)*q*cos(2*pi*1e6*t)*4*0.01*y(1)^3)];

=0.8834+((0.9325-0.8834)/0.0018)*0.001215
=0.91658
當加入
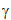 項時且octopole值為 -1%,Mathieu equation的表示如下;
項時且octopole值為 -1%,Mathieu equation的表示如下;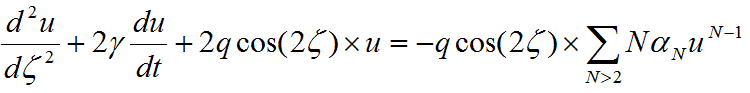
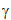 是氣體阻尼系數(damping)的表示值,大約0.005,不同壓力與氣體分子會有所不同。
是氣體阻尼系數(damping)的表示值,大約0.005,不同壓力與氣體分子會有所不同。function dy=func13_7(t,y)
q=0.88+((0.932-0.88)/0.0018)*t
dy=[y(2);-((((2*pi*1e6)^2)/2)*q*cos(2*pi*1e6*t)*y(1))-0.005*y(2)+((((2*pi*1e6)^2)/4)*q*cos(2*pi*1e6*t)*4*0.01*y(1)^3)];

結論
Ring上有洞或end cap有洞以及truncation的距離都會造成-1% octopole項的產生,使得解析度變差,truncation的距離至少2倍r0。當octopole項為+1%時沒有出現延遲拋出(delay ejection)的問題,這也是為何將end cap的拋物面改成拉伸,z0=0.70711*110.6%=0.78206,如此可以低消end cap挖洞所造成的-1% octopole項。
參考文獻
[1] M. Sudakov, International Journal of Mass Spectrometry 206 (2001) 27.[2] Z. Nie et al. International Journal of Mass Spectrometry 270 (2008) 8.
[3] Alexander A. Makarov, Anal. Chem., 68, (1996), 4257.
